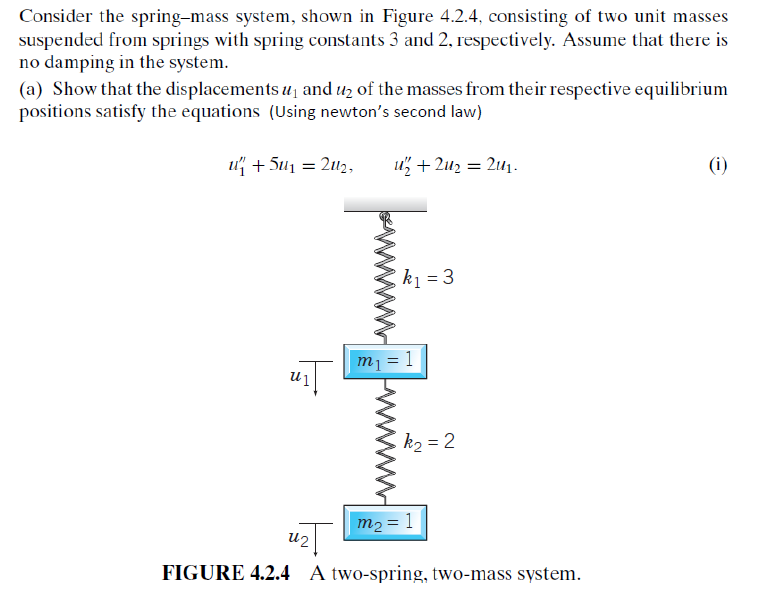
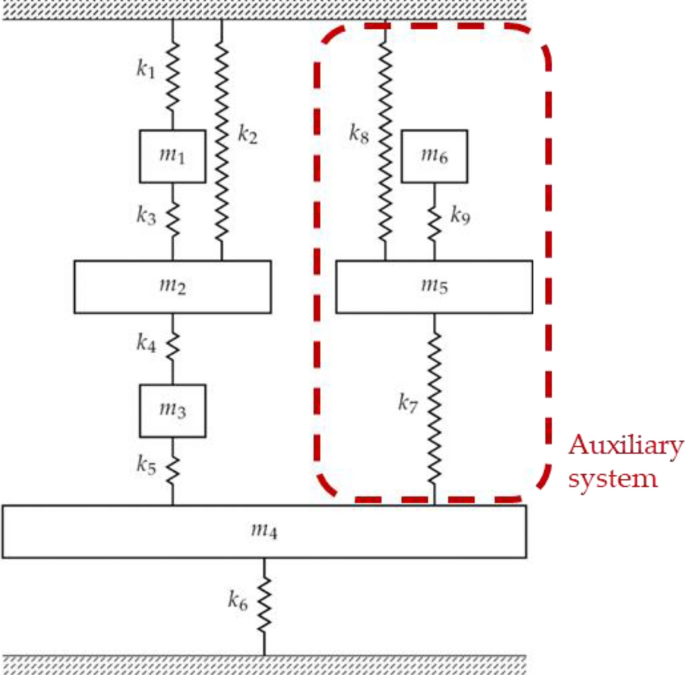
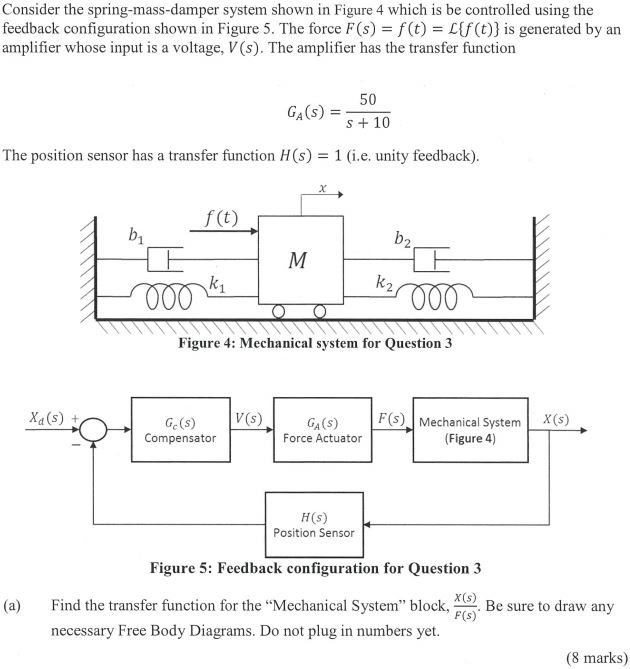
Consider The Spring Mass System Shown In Figure 424
Solved Consider The Spring Mass System Shown In Figure Chegg Com
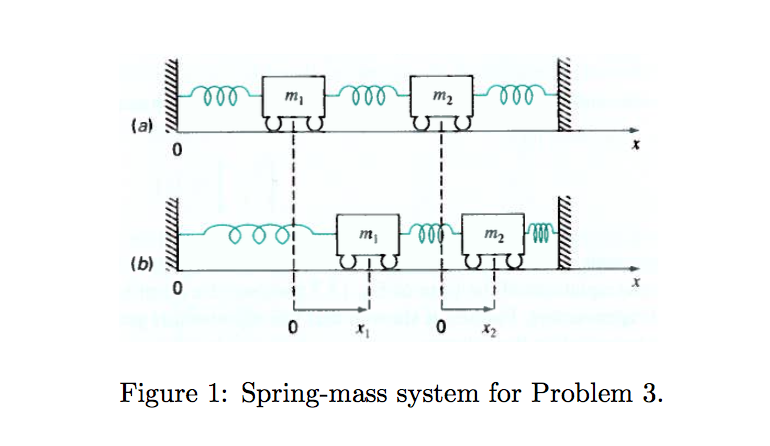
Consider the spring mass system shown in figure 424. 111 Consider the mass-on-a-spring system shown in the figure. But okay So far apart theyre here. The spring-mass system can also be used in a wide variety of applications.
The mass m is supported by a spring of stiffness k and is excited by a dynamic force ft. Assuming no friction in the pulley find the maximum elongation of the spring. A spring-mass system in simple terms can be described as a spring sytem where a block is hung or attached at the free end of the spring.
The system shown in the figure consider of a light inextenslible cord light frictionless pulley and blocks of equal mass. The spring-mass system can usually be used to find the period of any object performing the simple harmonic motion. A mass m is suspended from a spring of stiffness 4000 Nm and is subjected to a harmonic force having amplitude of 10 N and a frequency of 5 Hz.
Assume that there is no damping in the system. Consider the spring-mass system shown in Figure 2. Consider the spring - mass system shown in Figure 424.
The spring-mass system of Question 4 It consists of a mass m attached to the lower free end of a spring as shown in Figure 3. Consider the spring-mass system shown in Figure 3 below. One Times Co sign of five p plus C.
Consider the springmass system shown in Figure 424 consisting of two unit masses suspended from springs with spring constants 3 and 2 respectively. At the equilibrium position the spring is relaxed. Consider the spring - mass system shown in Figure 424.
In addition find the amplitude four cycles later. Let us find out the time period of a spring-mass system oscillating on a smooth horizontal surface as shown in the figure 136.
Get Answer Consider The Spring Mass System Shown In Figure 4 2 4 Consisting Transtutors
Solved Consider The Spring Mass System Shown In Figure Chegg Com
Solved 1 Consider The Spring Mass System Shown In Figure 1 Chegg Com
Solved Consider The Spring Mass System Shown In Figure 4 2 4 Consisting Of Two Unit Masses Suspended From Springs With Spring Constants 3 And 2 Respectively Assume That There Is No Damping In The
Solved Consider A Spring Mass Damper System Shown Below Chegg Com
Solved Consider The Spring Mass System Shown In Figure 4 2 4 Consisting Of Two Unit Masses Suspended From Springs With Spring Constants 3 And 2 Respectively Assume That There Is No Damping In The
Solved Consider The Spring Mass Damper System Shown Below Chegg Com
Engineering Mechanics Ppt Download
Get Answer Consider The Spring Mass System Depicted In Figure Ap8 6 Develop Transtutors
Solved Consider The Spring Mass System Shown In Figure 1 Chegg Com
Aerostudents Com
Damped Mass Spring System With Two Degrees Of Freedom Download Scientific Diagram
Solutions Guides Com
Answered A Spring Mass System Shown In The Bartleby
For The Pulley Mass System Shown In Figure See Attached Image What Is The Acceleration Of Block A Quora
Solved Consider A Spring Mass Damper System Shown Below Chegg Com
Mec3403
Mrcet Com
Answered Nk M The Spring Mass System Shown In Bartleby
Solutions Guides Com
Beyond The Tuned Mass Damper A Comparative Study Of Passive Approaches To Vibration Absorption Through Antiresonance Assignment Springerlink
Pdf Free Vibration Of Spring Mounted Beams
Once Weekly Semaglutide In Adults With Overweight Or Obesity Nejm
1
Consider A Spring Mass Damper System Shown Below Chegg Com
Maintenance With Daratumumab Or Observation Following Treatment With Bortezomib Thalidomide And Dexamethasone With Or Without Daratumumab And Autologous Stem Cell Transplant In Patients With Newly Diagnosed Multiple Myeloma Cassiopeia An Open
Energies Free Full Text Dynamic Characteristics Of Downhole Bit Load And Analysis Of Conversion Efficiency Of Drill String Vibration Energy Html
Biomechanical And Biological Responses Of Periodontium In Orthodontic Tooth Movement Up Date In A New Decade International Journal Of Oral Science
All Surfaces Shown In Figure Are Smooth System Is Released With The Spring Unstretched In Equilibrium
Beyond The Tuned Mass Damper A Comparative Study Of Passive Approaches To Vibration Absorption Through Antiresonance Assignment Springerlink
Energies Free Full Text Dynamic Characteristics Of Downhole Bit Load And Analysis Of Conversion Efficiency Of Drill String Vibration Energy Html
Scielo Brasil Masps At The Crossroad Between The Complement And The Coagulation Cascades The Case For Covid 19 Masps At The Crossroad Between The Complement And The Coagulation Cascades
Source Apportionment Of Chlorinated Polycyclic Aromatic Hydrocarbons Associated With Ambient Particles In A Japanese Megacity Scientific Reports
Frontiers 3d Fem Soil Structure Interaction Analysis For Kashiwazaki Kariwa Nuclear Power Plant Considering Soil Separation And Sliding Built Environment
Cavity Optomechanical Sensing
Kdoqi Clinical Practice Guideline For Vascular Access 2019 Update American Journal Of Kidney Diseases
Solved Consider The Spring Mass System Shown In Figure 4 2 4 Consisting Of Two Unit Masses Suspended From Springs With Spring Constants 3 And 2 Respectively Assume That There Is No Damping In The
Hess The International Soil Moisture Network Serving Earth System Science For Over A Decade
Mechanics Map Undamped Free Vibrations
Biologically Active Secondary Metabolites From The Fungi Microbiology Spectrum
Kdoqi Clinical Practice Guideline For Vascular Access 2019 Update American Journal Of Kidney Diseases
Data Evaluation For Surface Sensitive Label Free Methods To Obtain Real Time Kinetic And Structural Information Of Thin Films A Practical Review With Related Software Packages Sciencedirect
Solved Consider The Spring Mass Damper System Shown In Chegg Com
Body Size And Digestive System Shape Resource Selection By Ungulates A Cross Taxa Test Of The Forage Maturation Hypothesis Esmaeili 2021 Ecology Letters Wiley Online Library
Evaluation Of Acidogenesis Products Effect On Biogas Production Performed With Metagenomics And Isotopic Approaches Biotechnology For Biofuels Full Text
Mec3403
Engineeringstatics Org
Energies Free Full Text Dynamic Characteristics Of Downhole Bit Load And Analysis Of Conversion Efficiency Of Drill String Vibration Energy Html
1
What is the frequency of this simple harmonic oscillator.
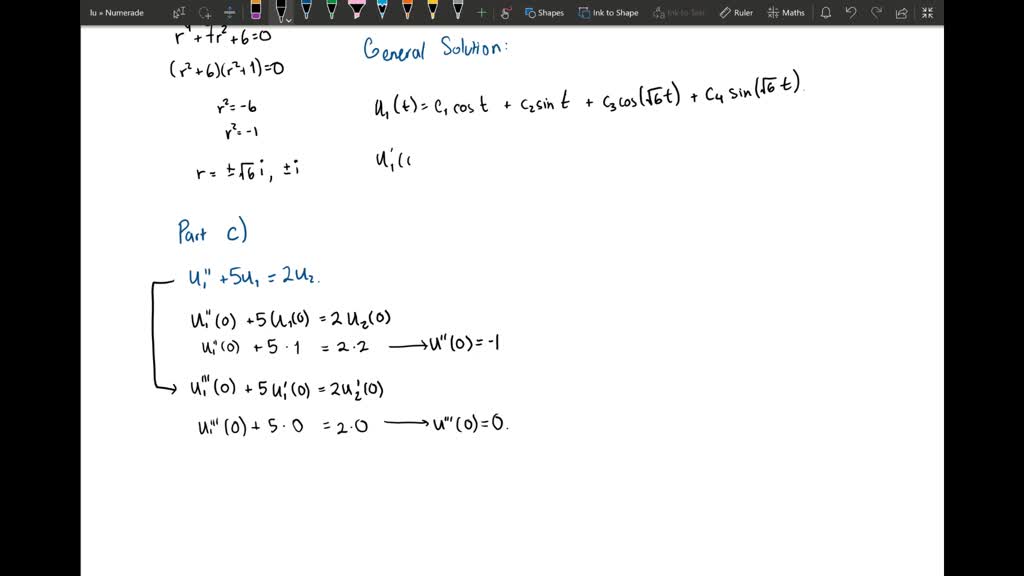
The basic vibration model of a simple oscillatory system consists of a mass a massless spring and a damper. The upper end of the spring is immovable and its mass is considered negligible. Initially the spring is unstretched when the system is released from rest. The spring-mass system of Question 4 It consists of a mass m attached to the lower free end of a spring as shown in Figure 3. A Show that the displacements u 1 and u 2 of the masses from their respective equilibrium positions satisfy the equations b Solve the first of Eqs. If the particle strikes thepan witha speed v find the speed with which the system moves just after the collision. The amplitude of the forced motion of the mass is observed to be 20 mm. Assume that there is no damping in the system. 4 pts b Assume the solution for each masssystem is of the general form it Ē A coswt B sinwt where ñ 1.
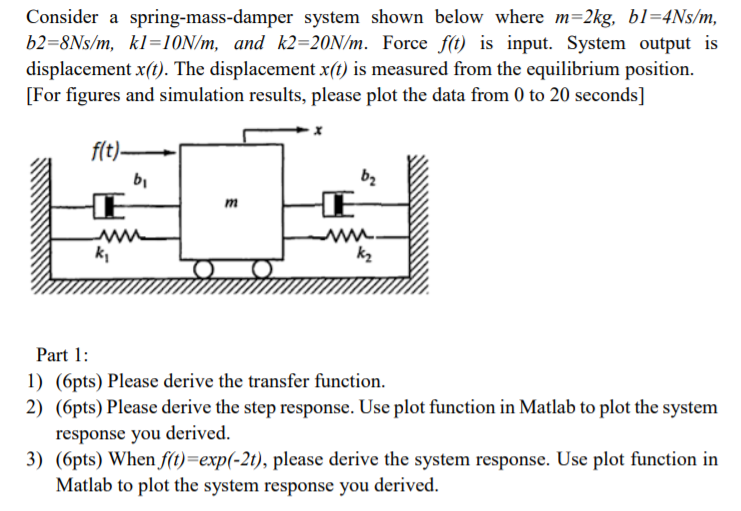
Assume that there is no damping in the system. Fyl kx R-bu F Focos wt mg Figure 3. A Show that the displacements u 1 and u 2 of the masses from their respective equilibrium positions satisfy the equations. In the system shown in Figure 5-59 the numerical values of rn b and k are given as rn 1 kg b 2 N-secm and k 100 Nm. 38 Hz Submit Answer Incorrect. Initially the systemis at rest when a particle of mass m falls on the pan and sticks to it. Mass-Spring-Damper Systems The Theory The Unforced Mass-Spring System The diagram shows a mass M suspended from a spring of natural length l and modulus of elasticity λ.
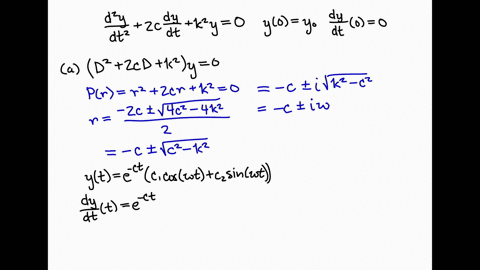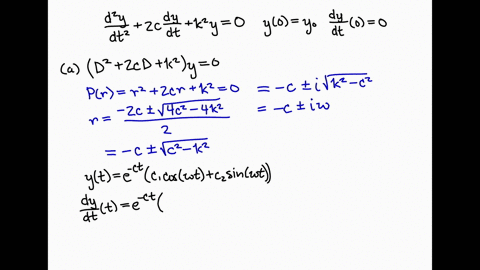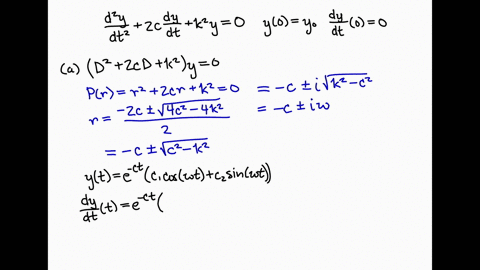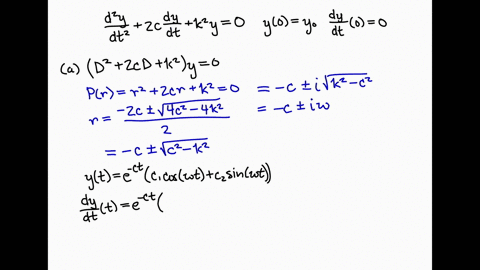
Post a Comment for "Consider The Spring Mass System Shown In Figure 424"